Trong phân tích dữ liệu chuỗi thời gian, một mô hình tốt được đưa ra khi phân tích trên các dữ liệu dừng. Hôm nay Trung tâm nghiên cứu định lượng xin giới thiệu cho các bạn về tính dừng của chuỗi thời gian và các kiểm định tính dừng.
1)Tính dừng
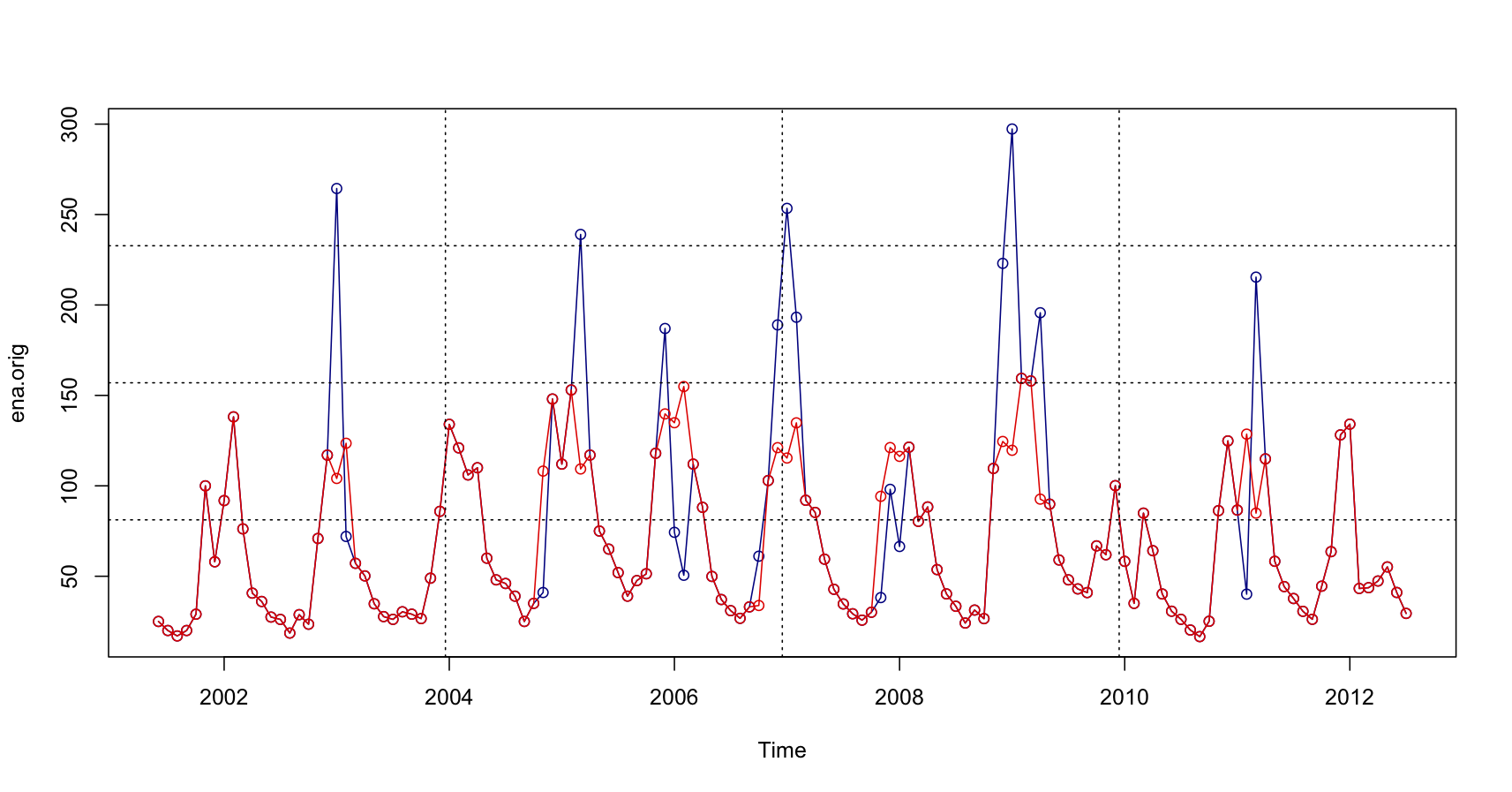
Theo Gujarati (2003) một chuỗi thời gian là dừng khi giá trị trung bình, phương sai, hiệp phương sai (tại các độ trễ khác nhau) giữ nguyên không đổi cho dù chuỗi được xác định vào thời điểm nào đi nữa. Chuỗi dừng có xu hướng trở về giá trị trung bình và những dao động quanh giá trị trung bình sẽ là như nhau. Nói cách khác, một chuỗi thời gian không dừng sẽ có giá trị trung bình thay đổi theo thời gian, hoặc giá trị phương sai thay đổi theo thời gian hoặc cả hai.
Có nhiều phương pháp kiểm tra tính dừng của chuỗi thời gian: kiểm định Dickey–Fuller (DF), kiểm định Phillip–Person (PP) và kiểm định Dickey và Fuller mở rộng (ADF), kiểm tra bằng giản đồ tự tương quan,… Phương pháp kiểm định này sẽ được trình bày phần tiếp theo đây.
2) Bậc tích hợp
Theo Ramanathan (2002) hầu hết các chuỗi thời gian về kinh tế là không dừng vì chúng thường có một xu hướng tuyến tính hoặc mũ theo thời gian. Tuy nhiên có thể biến đổi chúng về chuỗi dừng thông qua quá trình sai phân. Nếu sai phân bậc 1 của một chuỗi có tính dừng thì chuỗi ban đầu gọi là tích hợp bậc 1, ký hiệu là I(1). Tương tự, nếu sai phân bậc d của một chuỗi có tính dừng thì chuỗi ban đầu gọi là tích hợp bậc d, ký hiệu là I(d). Nếu chuỗi ban đầu (chưa lấy sai phân) có tính dừng thì gọi là I(0).
3) Kiểm định nghiệm đơn vị (Unit Root Test)
Kiểm định nghiệm đơn vị là một kiểm định được sử dụng khá phổ biến để kiểm định một chuỗi thời gian là dừng hay không dừng. Dickey và Fuller (1981) đã đưa ra kiểm định Dickey và Fuller (DF) và kiểm định Dickey và Fuller mở rộng (ADF). Nghiên cứu này sử dụng kiểm định ADF để thực hiện kiểm định nghiệm đơn vị nên chỉ tập trung vào lý thuyết của mô hình này. Cụ thể, theo Dickey và Fuller (1981) mô hình kiểm định nghiệm đơn vị mở rộng ADF có dạng:

Mô hình (2) khác với mô hình (1) là có thêm biến xu hướng về thời gian t. Biến xu hướng là một biến có giá trị từ 1 đến n, trong đó 1 đại diện cho quan sát đầu tiên trong dữ liệu và n đại diện cho quan sát cuối cùng trong chuỗi dữ liệu.
Nhiễu trắng là số hạng chỉ sai số ngẫu nhiên xuất phát từ các giả định cổ điển rằng nó có giá trị trung bình bằng 0, phương sai là hằng số và không tự tương quan.
Nghiên cứu sẽ tiến hành kiểm định trong cả hai trường hợp không có và có xu hướng về thời gian bằng cách sử dụng lần lượt các mô hình (1) và (2).
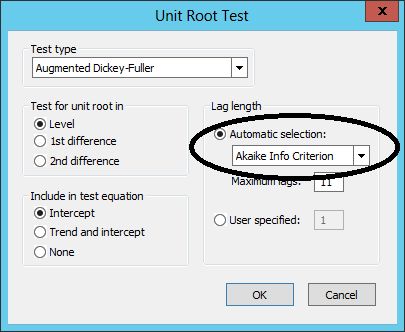
Kết quả của kiểm định ADF thường rất nhạy cảm với sự lựa chọn chiều dài độ trễ k nên tiêu chuẩn thông tin AIC (Akaike's Information Criterion) của Akaike (1973) được sử dụng để chọn lựa k tối ưu cho mô hình ADF. Cụ thể, giá trị k được lựa chọn sao cho AIC nhỏ nhất. Giá trị này sẽ được tìm một cách tự động khi dùng phần mềm Eviews để thực hiện kiểm định nghiệm đơn vị.
Giả thuyết kiểm định:
H0: β = 0 (Yt là chuỗi dữ liệu không dừng)
H1: β < 0 (Yt là chuỗi dữ liệu dừng)
Trong kiểm định ADF, giá trị kiểm định ADF không theo phân phối chuẩn. Theo Dickey và Fuller (1981) giá trị t ước lượng của các hệ số trong các mô hình (3.1) và (3.2) sẽ theo phân phối xác suất τ (tau statistic, τ = giá trị hệ số ước lượng/ sai số của hệ số ước lượng). Giá trị tới hạn τ được xác định dựa trên bảng giá trị tính sẵn của Mackinnon (1996). Giá trị tới hạn này cũng được tính sẵn khi kiểm định ADF bằng phần mềm Eviews. Để kiểm định giả thuyết H0 nghiên cứu so sánh giá trị kiểm định τ tính toán với giá trị τ tới hạn của Mackinnon và kết luận về tính dừng của các chuỗi quan sát. Cụ thể, nếu trị tuyệt đối của giá trị tính toán lớn hơn trị tuyệt đối giá trị tới hạn thì giả thuyết H0 sẽ bị bác bỏ, tức chuỗi dữ liệu có tính dừng và ngược lại chấp nhận giả thuyết H0, tức dữ liệu không có tính dừng.
Duynv
duynguyen.qa@gmail.com
















![KHÓA HỌC PHÂN TÍCH DỮ LIỆU CƠ BẢN VỚI R [27/6/2020] KHÓA HỌC PHÂN TÍCH DỮ LIỆU CƠ BẢN VỚI R [27/6/2020]](https://nghiencuudinhluong.com/apps/timthumb/timthumb.php?src=https://nghiencuudinhluong.com/uploads/bai_viet/flat550x550075fu4.jpg&w=77&h=56&q=75)



Thư điện tử của bạn sẽ không được hiển thị công khai. Các trường bắt buộc được đánh dấu *